14
Dec
Linear Algebra Series - Change of Basis Matrix Solver
Interactive Solver for the Change of Basis Matrix
6 min read
linear-algebra-series
14
Dec
Linear Algebra Series - The Four Fundamental Subspaces Solver
Interactive Solver for The Four Fundamental Subspaces - Column Space, Row Space, Null Space and the Left Null Space
5 min read
06
Dec
Linear Algebra Series - Special Topics
We round out the course with advanced frontiers. From Jordan Canonical Forms for defective matrices to an introduction to Tensors, these topics bridge the gap between standard linear algebra and advanced theoretical physics or machine learning research.
8 min read
06
Dec
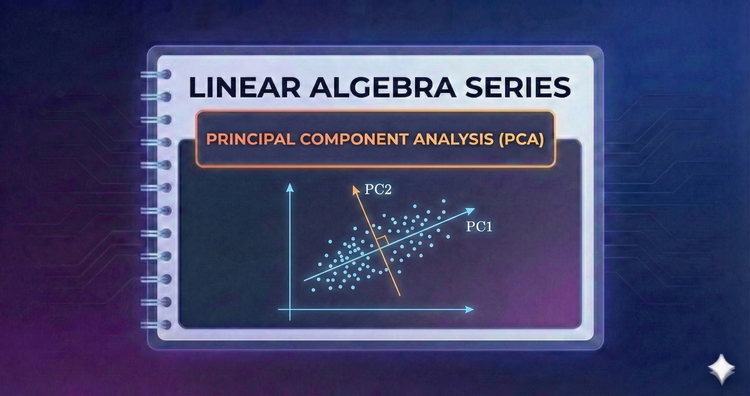
Linear Algebra Series - Principal Component Analysis (PCA)
In the age of Big Data, we have too many variables. PCA uses linear algebra to reduce dataset dimensionality while keeping the most important information, simplifying complex data clusters into understandable, actionable patterns.
8 min read
06
Dec
Linear Algebra Series - Singular Value Decomposition (SVD)
The pinnacle of linear algebra, SVD works on any matrix. We learn to break a matrix into strictly orthogonal components, a technique crucial for image compression, noise reduction, and modern recommendation systems.
9 min read
06
Dec
Linear Algebra Series - Symmetric Matrices and Quadratic Forms
Symmetric matrices appear frequently in physics. We explore the Spectral Theorem, which guarantees beautiful orthogonal properties, and use them to analyze the geometry of Quadratic Forms to visualize ellipsoids, paraboloids, and saddles.
8 min read
06
Dec
Linear Algebra Series - Diagonalization
Complex systems are hard to analyze when variables interact. Diagonalization uncouples these dependencies, transforming a tangled matrix into a simple diagonal form that makes computing high powers and predicting long-term trends trivial.
8 min read
06
Dec
Linear Algebra Series - Eigenvalues and Eigenvectors
Most vectors change direction when transformed, but Eigenvectors stay on path. Finding these vectors and their scaling factors (Eigenvalues) unlocks the "DNA" of a matrix, explaining system stability, vibration modes, and growth patterns.
8 min read
06
Dec
Linear Algebra Series - Projections and Approximations
Real-world data is rarely perfect. When exact solutions are impossible, we use Orthogonal Projections and Least Squares to find the "best possible" approximation—the mathematical foundation of linear regression and data fitting.
8 min read
06
Dec
Linear Algebra Series - Inner Product Spaces
Geometry requires measurement. By generalizing the dot product, we gain the ability to measure lengths and angles in abstract spaces, defining precisely what it means for two complex functions or signals to be perpendicular (orthogonal).
8 min read