Probability & Statistics - Expectation and Variance
We summarize distributions using two key metrics: Expectation (the "center of gravity" or long-run average) and Variance (the spread or volatility). Together, these moments provide a snapshot of a variable's central tendency and reliability.
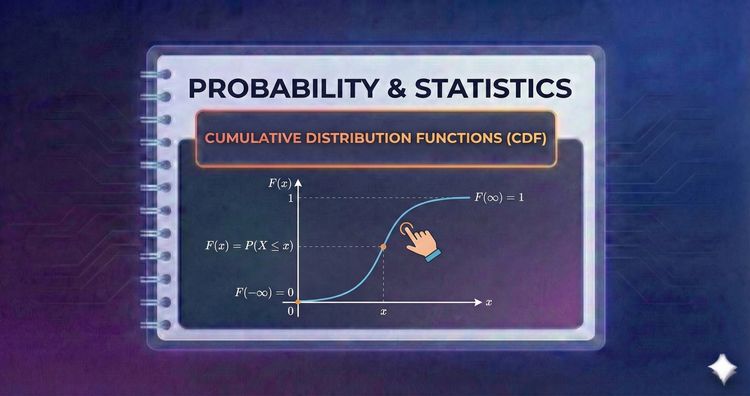
Probability & Statistics - Cumulative Distribution Functions (CDF)
The CDF answers "what is the probability that X is less than or equal to x?" By accumulating probabilities across the number line, it provides a complete view of a distribution, unifying discrete steps and continuous curves under one definition.
Probability & Statistics - Probability Mass Functions (PMF)
For discrete variables, the PMF assigns a probability to every distinct outcome. It acts as a frequency map, allowing us to visualize exactly how probability is distributed across countable values, such as dice rolls or daily sales figures.
Probability & Statistics - The Concept of a Random Variable
A random variable is a function that maps abstract outcomes (like a coin flip) to real numbers. This abstraction bridges the gap between descriptive events and quantitative analysis, allowing us to apply algebraic tools to uncertain processes.
Probability & Statistics - Bayes’ Theorem
A powerful tool for reversing conditional probabilities. Bayes' Theorem lets us update our beliefs (priors) after observing new evidence (likelihoods). It is fundamental to diagnostic reasoning, modern data science, and AI decision-making.
Probability & Statistics - Independence
Two events are independent if the occurrence of one provides no information about the other. We will define independence mathematically and distinguish it from mutually exclusive events to avoid common logical pitfalls.
Probability & Statistics - Conditional Probability
Events rarely happen in a vacuum. We examine how the probability of an event changes when we know another has already occurred. This concept allows us to update predictions based on partial information or restricted sample spaces.
Probability & Statistics - Counting Techniques
To calculate probabilities, we often need to count complex possibilities first. We will master permutations (where order matters) and combinations (where order doesn't) to solve problems involving large arrangements, selections, and distinct groupings.
Probability & Statistics - The Axioms of Probability
Kolmogorov’s axioms provide the rigid mathematical rules that all probabilities must obey. We’ll explore how the principles of non-negativity, normalization, and additivity ensure that our probability models remain consistent, logical, and mathematically sound.
Probability & Statistics - Sample Spaces and Events
The foundation of probability lies in set theory. We define the sample space as the set of all possible outcomes, while events are specific subsets. Understanding unions, intersections, and complements is crucial for quantifying real-world uncertainty.